About
Net is a free game by Simon Tatham, and in my opinion, it's insanely addictive; it is part of his collection of puzzles. This page lists a series of strategies for beating it that I've found.
The objective of the game is to get fluid to flow from a central node (
) and out to all the other nodes (
) by way of pipes (
, 
, and 
; I call the three types of pipes bent, straight, and three-way, respectively). These are arranged and randomly scrambled in a grid and the individual tiles must be rotated to make the fluid flow correctly. On some grids it's possible to light up all the nodes without using all the pipes, but a successful game depends on all tiles being lit up. Here's an example of an unsolved game:
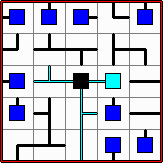
And the same game, only solved:
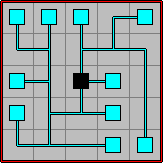
The greyed-out tiles are tiles whose position you know must be so; they can't be rotated (unless you unfreeze them). It's important to know that there can be no loops and that there can be no leaks (all exits on a tile must be utilized). This is a loop:
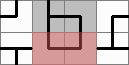
And here it has been corrected:
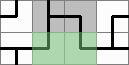
Similarly, here's a leak:
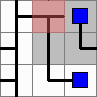
And the corrected version of it:
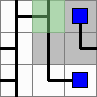
It's useful to note the binary nature of the tiles' sides: They either have entry points, or they don't. For instance, a node has one entry point (hence three of its sides are blocked); a three-way pipe has three entry points (hence one blocked side). The corollary is that once you know a tile's position, you can avoid leaks by making sure that the entry points of adjacent tiles don't point to the known tile's blocked sides. Consider the following:
In all but the last case, there are leaks. Hence there is only one position for the three-way pipe where it doesn't produce a leak.
Controls
The game can be controlled by both mouse and keyboard.
Mouse
Left-clicking a tile will rotate it counter-clockwise. Right-clicking a tile will rotate it clockwise. Middle-clicking or shift-clicking a tile will grey it out so that you won't accidentally rotate it.
Keyboard
At first I played Net with the mouse, but if you can get used to the keyboard you'll soon zip through the grids like a surge of power on crack.
The selector is moved with the arrow keys. a moves the currently selected tile counter-clockwise, d moves it clockwise, s greys it out, and f rotates it 180 degrees (I've never found the f key particularly useful). By holding down ctrl and using the arrow keys you can move the central node around. If the walls wrap around, holding down shift and using the arrow keys lets you pan across the grid (very useful). The q key quits the game. The j key scrambles tiles which aren't greyed out (I've never found a use for this).
Strategies
Edges
You should start with the edges (unless "Walls wrap around" is checked, in which case there are no edges). All straight and three-way pipes have unambiguous solutions, so you should start with these:
And here it is, solved:
Notice that there's only one position these can be in to avoid leaks. The position of the nodes can be inferred from the positions of the pipes along the edge (again, because of the fact that there can be no leaks).
Islands
I call an isolated path of pipes and nodes an island. An example:
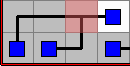
There can be no islands since every node needs to be connected to the central node. Here it's been corrected:
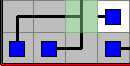
Notice that the highlighted tile couldn't be in any other position, as that would create a leak.
This is a very simple example, but the principle works for arbitrary sizes of islands, though it gets progressively harder to spot islands the bigger they are. Therefore, this strategy is only really useful at the start, or as a last resort on huge grids.
Here is another example of an island:
Fixing it is straighforward:
Fixing this second kind of island, for arbitrary sizes, is easy. Here's a slightly larger one, jumbled:
And here it is, fixed:
Notice, at the same time, that once you know a straight tile's position, adjacent straight pipes must be parallel to it to avoid leaks.
Linear repercussions
This is a strategy that works for bent pipes, when there are several of them in a "line" of tiles (that's why I call it linear). Here's the simplest example:
The bent pipe here can be in one of two positions:
or 
This is because in the two other positions, there's a leak against the wall:
or 
In either case, there's an exit on the right side, and there's a node right next to it, which means that to avoid a leak, the node has to connect to it:
Now, here's what I mean by linear repercussions. Consider this "line" of tiles:
Can we know something about the rotation of each tile? We can't know for certain how the bent tiles will be, but what about the three-way tile at the extreme? Remember that in each of the two positions in which a bent tile can be (to avoid a leak), the exit is at only one side. If you mentally (or actually, as I will do here for clarity) rotate the tiles along the "line", you'll see that we can solve the three-way pipe:
Node clusters
In clusters of nodes you can often solve a lot of them. The scenario is really a subset of the island scenario, but might not be immediately obvious: A node cannot point into another node, as that creates an island. Here's a node cluster:
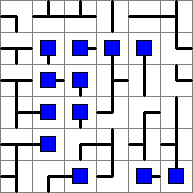
And here all the possible tiles have been solved:
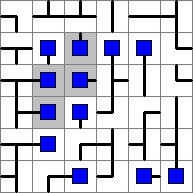
Notice that in any other position, each of the greyed-out nodes would point directly into another node.